名字贼长的玩意练习记录 Part. R703/04

 

注：* 号代表 VP（虚拟参赛）场。

1681E 2600 Labyrinth Adventures

题目大意

有一个 的方格图，坐标编号类似平面直角坐标系，左下角为 。

这个方格图被分成了 层，左下角 为第一层，随后每层都向外拓展一圈，如下图就是 的时候的情况：

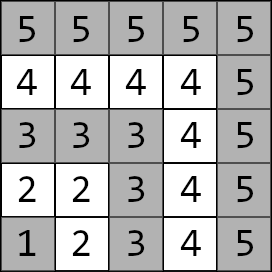
层与层之间有墙隔开，但每层都有两个门，分别分布在该层顶部和右侧，门是双向的。

现在给出这些门的坐标，有 次询问，每次给定两个坐标 和 ，请你回答两点之间的最短路。

解答

可以考虑将每一个门作为节点，一层一层的连边，建图。

然后现在就要求的是第 层的 2 个门和第 层的 2 个门之间的最短路。

最暴力的方法就是建图，每次查找的时候跑 Dijkstra。

而比较好的方法就是，使用线段树维护区间 ，里面记 ，表示门 到门 的最短距离。然后 pushup 的时候就枚举所有情况然后取最小值就可以了。

1428E 2200 Carrots for Rabbits

题目大意

新加坡动物园里有一些兔。为了喂养他们，管理员买了 根胡萝卜 。然而，兔很肥且繁殖很快。管理员现在有 只兔却没有足够的胡萝卜去喂它们。管理员需要把 根胡萝卜切成 根胡萝卜以喂养 只兔。出于某种原因，所有胡萝卜（包括切出来的胡萝卜）的长度必须为正整数。

兔很难拿稳大萝卜，也很难咽下大萝卜，所以吃掉一个长度为 的萝卜所需要的时间是 。

现在请你帮助管理员切这些萝卜，以最小化兔吃萝卜的总时间。

---

数据范围：

解答

这道题最开始和我一样想二分做法是没有前途的。

应该使用贪心算法。我们可以从 块胡萝卜一步一步地走到 块。具体步骤如下：

设 为将长度为 的胡萝卜切为 段的最小吃萝卜时间。这个东西可以直接算，因为最大值和最小值的差明显 。

那么就维护一个堆，堆里面 push 进所有的 。然后从 循环到 ，每次取值最小的堆元素，然后再 push 进 即可。

909D 2100 Colorful Points

题目大意

给你一组直线上的点。每个点都有一种颜色（用字母表示）。每个点最多有两个邻居，一个来自左边，一个来自右边。

您可以对这组点执行一系列操作。在一次操作中，我们会删除所有有一个与该点的颜色不同的邻居点的点。删除点是同时进行的，也就是说，首先确定哪些点需要删除，然后再删除它们。然后再执行下一个操作等。如果某个操作不会删除任何点，则不能执行该操作。

您需要执行多少次操作，直到下一次操作没有要删除的点为止？

。

解答

这道题暴力枚举的复杂度是 的，如何将其优化至 ？

回顾删点的过程。每一个点被删的条件是这个点不同于左右两个点的任意一个。所以可以把这些点分成若干个段，每一个段的颜色相同。比如样例 2 aabcaa 就可以被分为 。

然后对于每一个块，中间的块的左右两端点肯定要被删，所以长度 。在边缘上的块只用删除与中间接触的，所以长度 。

然后删除之后，就可以合并。这个可以使用 vector + pair<int, char> 解决。

每次操作的复杂度就是块的数量，而因为每一次要删除 个点，所以最终复杂度平衡下来就是 。

702E 2100 Analysis of Pathes in Functional Graph

题目大意

有一个 个点 条边的带权有向图（点编号 ），每个点有且仅有一条出边，对于每个点 求出由 出发走过 条边，这 条边权值的最小值与这 条边权值之和。

解答

我脑梗了。

倍增即可。

2074G Div.3 最新最热 Game With Triangles: Season 2

题目大意目前官方翻译没有出来。

解答

首先破环为 2 倍的链，然后可以区间 dp。设 为考虑区间 所可以搞出来的最大得分。然后最后答案就是所有 的 的 值即可。

然后就是最关键的转移：

1. 没有以 为两端点的三角形。。
2. 有以 为两端点的三角形。然后枚举中间端点 使其成为这个三角形的第三个端点。于是 。

然后答案就出来了。

想吐槽这场的 D 题的 pretest 真的太弱了，没开 long long 都能过 pretest，导致 FST。想把造数据的问候全家啊啊啊啊啊啊

CF553B Kyoya and Permutation 1900

题目大意

定义一个长度为的排列为仅由的元素组成，且每个元素恰好只出现次的序列。我们称数值在排列中的映射为。

Kyota Ootori 刚刚学习了排列的循环表示法。定义排列上的一个循环是一个由的一部分元素组成的序列，并且在这个序列中，任意一个元素在中的映射等于下一个元素（特别地，最后一个元素的映射等于第一个元素）。

显然，我们可以将一个排列划分成多个循环。例如可以被划分成，和三个循环。我们在每个循环周围加上括号，然后将它们连起来，得到的就是这个排列的循环表示法。例如的一种循环表示法是。

对于一个长度不为的排列，其循环表示法不是唯一的。为了使问题得到统一，我们定义一种标准循环表示法。即，对于每个循环，都将其最大值放在最前面，然后将这若干个循环按照最大值从小到大排列。这样，的标准循环表示法就是。

现在，Kyota 发现，如果我们去掉一个排列的标准循环表示法中的括号，我们将得到另一个排列。比如，由可以得到。

他还发现，将某些排列的标准循环表示法中的括号去除后，得到的排列和原排列是一样的。我们称这种排列为“好的排列”。他按字典序递增的顺序在纸上写下了长度为的所有好的排列，结果他的朋友 Tamaki Suoh 把这个列表搞丢了。Kyota 现在想要恢复这个列表。告诉你排列的长度以及，请你输出字典序从小到大第个好的排列。

，。保证长度为的，第个好的排列一定存在。

解答

容易发现，如果一个排列是好的排列，那么发生在每一个位置上的 swap 最多只有 1 次。并且 swap 是相邻两个数的。因为如果超过 3 个数的话除了原排列就没有别的了。

那么就可以设 为当 时，后面有多少种选法， 即当 ， 为当 。转移式从后往前，是容易推的。

然后求的时候因为保证一定存在，所以看 是否 。若是，则第 位铁定选 无疑了。否则，第 位选 ，第 位选 ，先让 ，然后使 。（所以这个 真的有用吗（））

CF750D New Year and Fireworks 1900

题目大意

烟花绽放时分为 层，每层会前进 格，当进入下一层是向左右 分开前进。 问在网格中，有多少网格至少被烟花经过一次？

。

解答

性质，性质，还是性质。这些低难题科技很少，大多数都是找性质。

正解其实很暴力。因为 ，所以烟花经过的范围最多也就 ，也就是 的范围。你用屁股维护信息都可以做出来。不想写了，这是口胡的做法。

CF463E Caisa and Tree 2100

题目大意

给你一个根为 的 （） 个节点的树，每个点有一个点权 。你需要进行 （） 个操作。操作类型如下：

• ，表示查询从 到根这条根链上是否有点 ，使 和 的 。若有，则输出 ，否则输出 。若存在多个答案，选择深度最大的 。
• ，即修改 。

保证 操作的数量不超过 。

解答

这道题评分两极分化了。CF 上面 2100，洛谷上面是紫提。（我不会打）可能洛谷认为的正解是别的东西，但是我这个方法切过去了，所以建议降绿/蓝。

首先，最明显的性质： 操作的数量 ，这启示我们修改可以先不用考虑，暴力重构都可以。

而且，因为修改数量 ，所以可以预处理答案，因为最坏情况下也只会重构 次，即预处理 次答案嘛。所以我们要考虑如何预处理，维护哪一些信息。

根据题目中所言「存在 」， 是什么，是两个数同时存在至少一个 的因数。也是两个数同时存在至少一个质因数。而众所周知，，大于 ，所以一个数的因数最多最多，也就只有 个。所以我们可以在预处理的时候，先 DFS 嘛，然后 DFS 到 的同时，维护一个数组 ，表示 这个质因数在 这一条链上最晚在哪一个节点里面出现（所以有一些下标会一直没有值）。然后先查 的质因数，作为这个点答案嘛，之后再更新 数组即可。预处理复杂度最多也就个 。然后 遍也就是 ，可以冲过去。就只是预处理每一个数的因数的时候耗费点时间，但是也最多就是 的复杂度。再加上查询是 的，时限也开的 ，这还不过去就没有道理了。（但是当初我怀疑内存会被卡

CF1147B Chladni Figure 1900

题目大意

稻中有一个圆盘，圆周长为 个单位。圆周被从 到 顺时针编号的 个点等分，这样 点和 点（ ）相邻， 点和 点也相邻。

圆盘上有 条直线，其端点都在上述 点中。

稻香想知道她的图像是否是旋转对称的，即是否存在一个整数 ( )，使得如果所有线段绕圆心顺时针旋转 个单位，新图像将与原始图像相同。

解答

首先，可以枚举因数，然后暴力 check。因为因数最多 个，所以时间复杂度正确。

但是因为标签里面有个字符串匹配，于是我就想可不可以用字符串。这里，我口胡了一个做法。因为现在已经 17:45 了所以准备回去看能不能实现。

我们处理每一个点连出去的点的距离集合，两个距离相同的集合就是同一种字符。（或者说可以使用其它方法分配字符？）然后分配字符完了后就可以找这个字符串是否存在周期，即循环节了。这个可以使用 KMP，我们求出 的 border，令其为 。那么因为 完全等于 ，所以可以设 为循环节，（其实可以证明如果成立那么 就是最小循环节。）那么只需要检查 是否可以整除 即可。即 是否可以整除 。（因为 ）

CF1257E The Contest 2000

题目大意

给出三个集合 ，分别有 个元素。设 ，三个集合里的所有元素两两不相同且在 之间，换句话说，这三个集合的并集恰好是 。

称将一个集合里的元素删除并加入到另一个集合中为一次操作。请用最少的操作次数使得：

• 包含 开头若干个元素（可以为空）；
• 包含 末尾若干个元素（可以为空）；
• 包含剩下的所有元素。

解答

首先，我们可以将全集分为 三段，第一段为 ，第二段为 ，第三段为 。设 为原本在集合 ， 的元素的个数。 为原本在集合 ， 的元素个数。原本的三个集合分别为 ；

那么我们可以得出来，对于每一对 ，答案为：

$$\begin{aligned} ans &= OutA_a + In(B + C)_a + OutB_b + (InC_b - InC_a)\\ &= Alen - InA_a + InB_a + Blen + (- InB_b + InC_b) \end{aligned}$$

容易发现和 有关的项只有 ，并且这个 其实可以预处理，所以就相当于是要在 范围内找 的最小值。使用线段树即可。所以最终只需要在 中枚举 ，然后代入取 即可。

CF2103D Div.2 最新最热 Local Construction

题目大意

数组 中的元素 ( ) 是局部最小值，如果以下条件至少有一个成立：

• 和 和 ，或
• 和 ，或
• 和 。

同样地，如果以下条件至少有一个成立，那么数组 中的元素 ( ) 就是局部最大值：

• 和 和 ，或
• 和 ，或
• 和 。

请注意，只有一个元素的数组不定义局部最小值和最大值。

有一个隐藏排列 。 长度为 。从操作 1 开始，交替对排列 进行以下两次操作，直到 中只剩下一个元素：

• 操作 1 - 删除 中所有不是局部最小值的元素。
• 操作 2 - 删除 中所有不是局部最大值的元素。

更具体地说，操作 1 在每次奇数迭代中执行，操作 2 在每次偶数迭代中执行，直到 中只剩下一个元素。

对于每个索引 ( )， 是元素 被删除的迭代次数，如果从未删除，则为 。

可以证明， 中最多经过 次迭代(换句话说， 次迭代)就只剩下一个元素。

给你一个数组 。你的任务是构造出满足数组 的 元素的任意排列 。

保证数组 合法。。

解答

这道题我赛时思路就想错了。

首先，因为迭代次数少于 ，所以可以直接暴力扫每一个数。

对于 ，因为它是第一次被删除的，所以我们尽量要让他更大。所以就从 开始赋值。但是还有一个问题就是边界问题。那么肯定是要左边的 的 递减，然后右边的 的 递增。我们可以定中间的 为界。意思就是，先顺序遍历，把 左边的 从大到小赋值，然后再倒序遍历，把 右边的 从大到小赋值。

对于 ，因为它是第二次被删的，所以我们尽量要让他更小。使用类似 的方法，从 开始赋值。先顺序，把 左边的 从小到大，然后倒序，把 右边的 从小到大。

然后 。因为之前最大的已经赋过了，所以就从没有赋过的最大的值开始赋，和 同样的方法。 也是一样。然后就这么赋下去……

直到最后只剩下一个 。最后没有使用的数就赋给它。结束。

CF2103E Div.2 最新最热 Keep the Sum

题目大意

给你一个整数 和一个长度为 的数组 ，其中每个元素都满足 的所有 。您可以对数组执行以下操作：

• 选择两个不同的索引 和 ( 和 )，使得 .
• 选择满足 的整数 。
• 将 减少 ，将 增加 。换句话说，更新 和 。

需要注意的是， 上的约束条件确保数组 的所有元素在整个操作过程中保持在 和 之间。

你的任务是确定是否有可能通过上述操作使数组 非递减 。如果可能，请找出一个最多包含 次操作的数列序列，将数组转化为非递减数组。

可以证明，如果可以通过上述操作使数组非递减，则存在一个最多使用 次操作的解。

如果对于所有的 数组 都成立 ，则称数组 为非递减数组。

解答

又是一道构造题……

首先，判定何时无解。那么肯定是不存在任何一对 使 ，并且原序列不是单调不降时。那么我们假设其他情况一定有解。

发现我们可以为了让这个序列有序，可以使用次数为 的排序操作。如何 次？可以每次找一个最小的，把它交换到最前面去。然后找次小的，把它交换到第二前面去……以此类推。

如何实现交换操作？设现在有 四数，，并且现在欲交换 。那么可以首先变为 ，然后变为 ，最后变为 。前面两个数具体是什么不重要，因为只要和为 ，就可以交换两个数。

所以我们要尽量让前面两个数固定下来，不用最后再交换它们的位置。发现可以将这两个数分别放在第一个位置，值为 ；和最后一个位置，值为 。根据题意，可以发现这一定是最小值和最大值。然后再执行交换操作。

那么假设现在有 四数，现欲将 分别赋为 。可以做以下操作：。

CF1762D 2100 GCD Queries

题目大意

这是一道交互题， 组数据。

有一个 的排列 。你可以进行以下询问最多 次：

• ? i j：询问 和 两个元素（），交互器会返回两个元素的 。

询问以后，你需要给出两个下标 （可以相等），满足 或 ，格式为 ! x y，如果答案正确，交互器会返回 ，否则返回 。注意程序需要读入结果！

。

解答

根据 的性质，我们可以得出：

• 当 ，。因为若 ， 互不相等得出来的结果会不一样，矛盾。
• 当 ，。因为若 ，，又因为 ，故矛盾。
• 当 ，。原因同理。

只需询问 次即可。

CF1167F Scalar Queries 2300

题目大意

给出一个数组 ，其中所有元素两两不同。

定义函数 ：

• 定义数组 ，其中
• 将按从小到大排序
• 则此时函数的值是

请计算对于所有满足 的 和 ， 的和。

由于结果可能很大，请输出对 取模的值。

, , 所有 两两不同。

解答

我们可以对每一个数拆开算贡献。

对于数 ，它对答案的贡献就是所有区间内它的排名之和再乘上它的值。我们定义 。则它的排名之和为 。发现是个加法式，可以将其拆开。

第一项为 ，第二项为 ，第三项为 。

如何快速求第一项和第二项？我们令 ，即第一项，发现所有 的数，每一个数会给 造成 的贡献。这个可以使用树状数组维护。

最后综合答案即可。

CF2106G1, G2 Div.3 最新最热 Baudelaire

题目大意

交互题。

波德莱尔非常富有，因此他买了一棵大小为 的树，树根位于某个任意节点。此外，每个节点的值都是 或 。

书呆子牛看到了这棵树，并爱上了它。但是，计算机科学专业的薪水不够高，所以他买不起这棵树。波德莱尔决定和书呆子牛玩一个游戏，如果他赢了，就把这棵树送给他。

牛呆子不知道哪个节点是根，也不知道节点的值。不过，他可以向波德莱尔提出两种询问：

• :设 为从树根到节点 的路径上所有节点的值之和。牛书呆子可以选择一个整数 。 和 节点 ，他将得到值 。
• :波德莱尔将切换节点 的值。具体来说，如果 的值是 ，它就会变成 ，反之亦然。

如果 “牛书呆子 “在 次查询中猜对了每个节点的值(即查询后最终树的值)，那么他就赢了。你能帮助他获胜吗？

。

简单版：整棵树是以 为中心点的菊花，但是 不一定是根。

困难版：整棵树形态任意。

解答

本解答分为简单版和困难版两版。

---

对于简单版，我们可以分成两段：首先求出树根，然后根据树根推出所有点的权值。第二段是容易的，查询次数 次。现在要在 次以内确定树根。

由于查询的是 的和，并且整棵树的形态非常的特殊，那么就只有两种情况：一是节点 就是根节点，二是根节点是节点 的父节点。那么我们考虑在菊花的花瓣上面找节点 的父节点，如果找不到那么节点 就是根节点。

因为点 是除了根节点的其它点都要经过的点，所以我们可以先查询区间 的 ，然后修改点 权值，最后再查询区间 的 。如果两次的差值的绝对值 ，那么就说明 的所有点的祖先都含有 ，也就是它们没一个是根节点，否则，如果 ，那么说明 里含有根节点。于是，我们就可以二分 区间，然后看找不找得到根节点（找不到根节点的标志是 ）。如果找得到，那么爽，找不到，就说明根节点是 。询问次数 。

找到根节点后，先把所有点权值问一遍，然后 DFS 一下树就可以得出权值了。

---

然后对于困难版，我们需要执行类似简单版的操作。

可以考虑先选一个关键点，然后对这个点执行问询，问询出这个点的父节点是哪个（如果没有就说明这个点是根）。然后其它儿子就都消失掉，然后再在父节点的连通块里面选一个关键点继续问询……直到这个关键点没有父节点（即这个关键点为根）或是这个关键点没有邻居。

容易想到我们需要选取这个树的重心作为关键点，因为这样做每一次操作至少会使一棵树的大小减去一半。那么总询问次数就是 。符合题目要求。

CF2040E* 2100 Control of Randomness

题目大意

给定一棵树，树上有 个顶点。

我们在某个顶点 放置一个机器人，最初拥有 枚硬币。以下是机器人的移动规则：

• 当 为奇数时，机器人会向顶点 的方向移动到相邻的节点。
• 当 为偶数时，如果你愿意支付一枚硬币并且还有剩余的硬币，则机器人会向顶点 的方向移动到相邻的节点；否则，机器人将随机选择一个相邻的节点移动。

当机器人到达顶点 时，过程终止。记 为通过最佳策略使用硬币时，使得上述过程的期望步数最小值。

你的任务是解决 个查询。每个查询包含一对 ，你需要计算 模 的值。

具体来说，令 。结果可以表示为一个不可约分数 ，其中 和 是整数且 。你需要输出 。换句话说，输出满足 且 的整数 。

保证输入的边构成一棵树，并且所有测试用例的 之和不超过 ， 之和不超过 。

解答

诈骗期望。根本不需要。

我们可以把奇偶操作放到一起看，把两个操作合为一个整体。

那么首先考虑不使用硬币，设波特初始时所在的点为 ，那么波特最终走到的点会是 或 （包括 ）。因为随机是等概率随的，所以每一种情况的概率都是 。那么走到 要期望随机 次，即期望走 步。

而如果使用硬币，那么这一轮它会直接走到 ，期望步数 步。

于是我们可以暴力跳爷爷，然后对于每一个点都记录 ，然后排序，取前 （硬币个数）大将它们赋为 最后求和即可。

而在跳爷爷的过程中若遇到 ，那么期望步数 步。结束。

F 题是 Burnside 引理会不了一点