3 月做题记录

 

P10238 PANDORA PARADOXXX Re:Master Lv.15

题目大意

给定一棵 个结点的树。一棵树被定义为一个有 个点和 条边的无向连通图。这棵树的边有边权。两点 间的距离 定义为从 到 的简单路径边权和。可以证明树上两点间的简单路径是唯一的。特别的，我们规定 。

现在有 次操作，每次会删除这棵树上的一条边。显然在做出至少一次操作后，这棵树会被分成若干个连通块。你需要在每次操作后都求出每个连通块内距离最远的两个点的距离的最大值。

形式化的，每次操作后，你要求出

$$\max\limits_{c \in C}\{\max\limits_{u, v \in c} \mathrm{dist}(u,v)\}$$

其中 表示当前所有连通块构成的集合。

解答

用人话来说就是给一棵树，每次删边，求所有连通块里最大的直径。

删边之后求直径不好搞，可以考虑正难则反，时光倒流，从后往前加边。

那么我们就可以首先得到一些树形的连通块，然后用两次 DFS 求出这些连通块的直径。

每次用一条边合并两个连通块，然后更新大小较小的连通块的信息，再对于这个新的连通块求新的直径长度。而现在我们要实现的就是如何快速求这个新的直径长度。

假设我们已知之前的那两个连通块的直径分别为 和 。那么新的直径有 3 种情况：

• 这种情况肯定是一条直径连接了两个连通块。那么肯定经过了连接两个连通块的那条边。设这条边为 。

  要使这个直径最长，那么第一个端点肯定要选 所在的连通块里距离 最大的一个点，第二个端点肯定要选 所在的连通块里距离 最大的一个点。

  而我们知道，两次 DFS 求直径的方法里的第一次 DFS 之后就是拿的距离最大的一个点作为树的直径端点之一。所以第一个端点肯定是 的直径的一个端点，第二个端点同理。

于是，就得到了一个性质，新直径的两个端点一定是 的其中两个，即原来两个直径的四个端点的其中两个。

利用之前维护的性质，可以在树上记录每一个点到根的距离 和求 LCA 来求出两点之间的距离。然后新的直径就可以确定出来了。

然后倒序记录答案，最后输出答案即可。记得多测要清空！

0313T1 xor / LOJ6060 Set

题目大意

给出 个非负整数，将数划分成两个集合，记为一号集合和二号集合。 为一号集合中所有数的异或和， 为二号集合中所有数的异或和。在最大化 的前提下，最小化 。

解答

我们可以首先求出所有 的异或和，记其为 。然后我们要选出一些数的异或和组成数 ，目标要使 最大。

于是，我们可以对 考虑每一位。

• 若 （即 的第 位为 ），那么我们一定从高位到低位地，希望 的这一位为 。
• 而若 ，那么不管 的这一位取 ，对 的答案都无影响。而因为我们要最小化题面中的 ，并且之前要希望 最大，所以这里可以转化为，令 。要使 最小， 最大，所以我们要使 的这一位为 。

而因为是在最大化 的前提下最小化 ，所以就要把所有的元素根据位重组。假设 ，那么这些元素就要根据 的顺序重组然后插到线性基里面。

然后求最大异或和，然后再转回来，最后跟 异或一下就可以了。

P5355 由乃的玉米田 Master

题目大意

给你一个序列 ，长度为 ，有 次操作，每次询问一个区间是否可以选出两个数它们的差为 ，或者询问一个区间是否可以选出两个数它们的和为 ，或者询问一个区间是否可以选出两个数它们的乘积为 ，或者询问一个区间是否可以选出两个数它们的商为 （没有余数） ，这四个操作分别为操作 。

选出的这两个数可以是同一个位置的数。

所有输入的数在 内，序列中的元素在 内。

弱化版（只有加、减、乘操作）：P3674 小清新人渣的本愿 Master

解答

首先，我们可以使用莫队离线。那么分成 4 个操作分别考虑：

• 查询差为 ：我们建一个 bitset，vis[b] = 1 表示 这个数在 里面出现过。那么因为查询差为 ，。所以可以把这个 vis 右移 位，再与一下看是否有值即可。

• 查询和为 ：因为 ，所以我们再建一个 bitset，revis[b] = 1 表示 这个数在 里面出现过。 是给定的一个阈值，需大于等于所有数的最大值。令 。

  然后式子就变成了 。所以让 revis 右移 位，然后再与一下 vis 看是否有值即可。

• 查询积为 ：因为枚举一个数的因数的复杂度最多 ，所以暴力枚举因数，再用 vis 判一下即可。

• 查询商为 ：这个和前面的就都不一样了。可以对这个商进行根号分治，当 时，直接暴力枚举 和 ，看是否同时存在即可。

  否则，，就要考虑另一种方法了。因为 的复杂度是可以接受的，所以我们可以直接对于每一个 考虑，然后枚举所有的数。

  具体来说，就是首先把 的全部拎出来，然后枚举 。对于每一个位置，记录 表示最近的存在 这两个数的左端点的最大值。然后对于每一个位置更新的时候，动态维护 表示 这个数上一次出现在哪里。然后枚举是否存在 和 这两种情况，更新答案即可。注意因为可以选两个相同的数，所以 应该在枚举到 时及时被更新。

P11307 Pristojba Master

题目大意

有一张 个点的简单无向图 。

给定数列 ，边 （）的边权为 。

然而，不是所有 间都有边连接。给定 个三元组形如 ，表示「， 间有边连接」。

求出这张无向图的最小生成树的边权和。

解答

一般的，如果这个图的边数相对较多，我们就放弃 Kruskal 算法，转用 Boruvka 算法。

我们对于每一个点，存储其有连边的点的点权最小值，设其为 、以及和 颜色不同的点权次小值。合并两个点的时候就分情况讨论 合并即可。这样，你最小生成树连边就只会在这两个里面选一个了。

然后因为一个点它连向了很多个区间，所以可以使用区间查询数据结构（比如线段树）来查询它连向的那些点的最小、颜色不同次小值。并且，会有一些点的区间包含它，就再建一棵线段树，看是哪些点连向了它。最后将这两棵树的答案合并。然后连边跑 Boruvka 即可。

因为每次会让最小连通块的大小至少 ，所以最多跑 轮。

P2048 [NOI2010] 超级钢琴 Master

题目大意

小 Z 是一个小有名气的钢琴家，最近 C 博士送给了小 Z 一架超级钢琴，小 Z 希望能够用这架钢琴创作出世界上最美妙的音乐。

这架超级钢琴可以弹奏出 个音符，编号为 至 。第 个音符的美妙度为 ，其中 可正可负。

一个“超级和弦”由若干个编号连续的音符组成，包含的音符个数不少于 且不多于 。我们定义超级和弦的美妙度为其包含的所有音符的美妙度之和。两个超级和弦被认为是相同的，当且仅当这两个超级和弦所包含的音符集合是相同的。

小 Z 决定创作一首由 个超级和弦组成的乐曲，为了使得乐曲更加动听，小 Z 要求该乐曲由 个不同的超级和弦组成。我们定义一首乐曲的美妙度为其所包含的所有超级和弦的美妙度之和。小 Z 想知道他能够创作出来的乐曲美妙度最大值是多少。

解答

一道非常牛的 RMQ 问题。

我们定义 为左端点为 ，右端点在 之间的超级和弦最大的美妙度。因为美妙度 定义是 ，而这个可以被转化为前缀和 ，所以 。而 可以使用 ST 表 求得。所以计算该函数所用的时间复杂度也自然就是 。

然后因为超级和弦音符个数在 之间，所以我们可以维护一个大根堆，首先把 给 push 进堆里面。然后查的时候就是查堆顶，也是可以 算出是哪一个 是最大值，之后，这个位置就不能用了。

我们把这个位置劈成两半，为 和 再 push 进堆里。（边界要判！）然后再查询即可。因为最多 push 次，所以时间复杂度正确，可过。

P8512 TEST_152 Master

题目大意

有一个操作序列。

现在，有 个询问 ,。

每次询问，你初始有一个长度为 的序列 ，初值全是 。

现在我们从 到 执行这 个操作。

每个操作是将 ~ 赋值为 。

询问所有操作结束后整个 的序列所有数的和。询问之间互相独立。

解答

因为这种区间赋值是经典的颜色段均摊操作，被删除的颜色段不会超过 个。所以可以使用 set 颜色段均摊。

但是这道题是有时间这一维度的限制。所以，我们可以先把询问以 为关键字离线，然后我们可以使用树状数组维护序列，删除颜色段 就在 减去 ，增加颜色段 就在 加上 ，最后求 区间和即可。

P4585 火星商店问题 Master

题目大意

火星上的一条商业街里按照商店的编号 ，依次排列着 个商店。商店里出售的琳琅满目的商品中，每种商品都用一个非负整数 来标价。每个商店每天都有可能进一些新商品，其标价可能与已有商品相同。

火星人在这条商业街购物时，通常会逛这条商业街某一段路上的所有商店，譬如说商店编号在区间 中的商店，从中挑选一件自己最喜欢的商品。每个火星人对商品的喜好标准各不相同。

通常每个火星人都有一个自己的喜好密码 。对每种标价为 的商品，喜好密码为 的火星人对这种商品的喜好程度与 异或 的值成正比。也就是说， 的值越大，他就越喜欢该商品。

每个火星人的购物卡在所有商店中只能购买最近 天内（含当天）进货的商品。另外，每个商店都有一种特殊商品不受进货日期限制，每位火星人在任何时刻都可以选择该特殊商品。每个商店中每种商品都能保证供应，不存在商品缺货的问题。

对于给定的按时间顺序排列的事件，计算每个购物的火星人的在本次购物活动中最喜欢的商品，即输出 的最大值。这里所说的按时间顺序排列的事件是指以下两种事件：

0 s v，表示编号为 的商店在新的一天新进一种标价为 的商品。 注意是先加天数，再在这一天进货。

1 l r x d，表示一位火星人当日在编号在 的商店购买 天内的商品，该火星人的喜好密码为 。天数不变。

对于 的数据，所有输入的整数在 范围内。

解答

我们可以使用树套树来维护。第一维维护商店区间，可以使用线段树维护。然后里面套 Trie 树，每一个节点维护能到达这个节点的最近的时间。不受日期限制的就是 。之后查询就在 Trie 树上面贪心查。修改和查询都是 。

P2414 [NOI2011] 阿狸的打字机 Master

题目大意

阿狸喜欢收藏各种稀奇古怪的东西，最近他淘到一台老式的打字机。打字机上只有 个按键，分别印有 个小写英文字母和 B、P 两个字母。经阿狸研究发现，这个打字机是这样工作的：

• 输入小写字母，打字机的一个凹槽中会加入这个字母(这个字母加在凹槽的最后)。
• 按一下印有 B 的按键，打字机凹槽中最后一个字母会消失。
• 按一下印有 P 的按键，打字机会在纸上打印出凹槽中现有的所有字母并换行，但凹槽中的字母不会消失。

例如，阿狸输入 aPaPBbP，纸上被打印的字符如下：

a
aa
ab

我们把纸上打印出来的字符串从 开始顺序编号，一直到 。打字机有一个非常有趣的功能，在打字机中暗藏一个带数字的小键盘，在小键盘上输入两个数 （其中 ），打字机会显示第 个打印的字符串在第 个打印的字符串中出现了多少次。

阿狸发现了这个功能以后很兴奋，他想写个程序完成同样的功能，你能帮助他么？

对于 的数据，，，第一行总长度 。

解答

因为有很多的子串和子串匹配，所以这道题可以选用 ACAM 或者是 SAM。这里用的是 ACAM。

建 ACAM 是好建的，根据题意操作即可。现在需要知道在 ACAM 上如何判定一个串 在另外一个串 中出现了多少次。

回忆一下 ACAM 如何判定一个串是否在另一个串中出现：

1. 沿着 ACAM 的边走。设现在遍历了 ，在点 。
2. 然后跳 的 树。若跳到了另一个字符串代表的节点，那么就说明存在另一个字符串，位置在 。

于是我们就转化为了：对于 个节点，分别在 AC 机上代表 ，问有多少个节点在 串所代表的节点在 树上的子树内。

因为求多少个符合条件的点在某个点的子树内这种问题，可以使用 dfn 序连续 + 区间查询解决。区间查询可以使用 BIT。然后我们每到一个新的节点，在 BIT 上单点加。每次删除节点，就跳到它的父亲，然后单点减。

然后对于询问，要在之前根据 将询问离线，然后在每一个 P 操作上查询即可。

P4306 [JSOI2010] 连通数 Expert

题目大意

度量一个有向图连通情况的一个指标是连通数，指图中可达顶点对个的个数。

如图

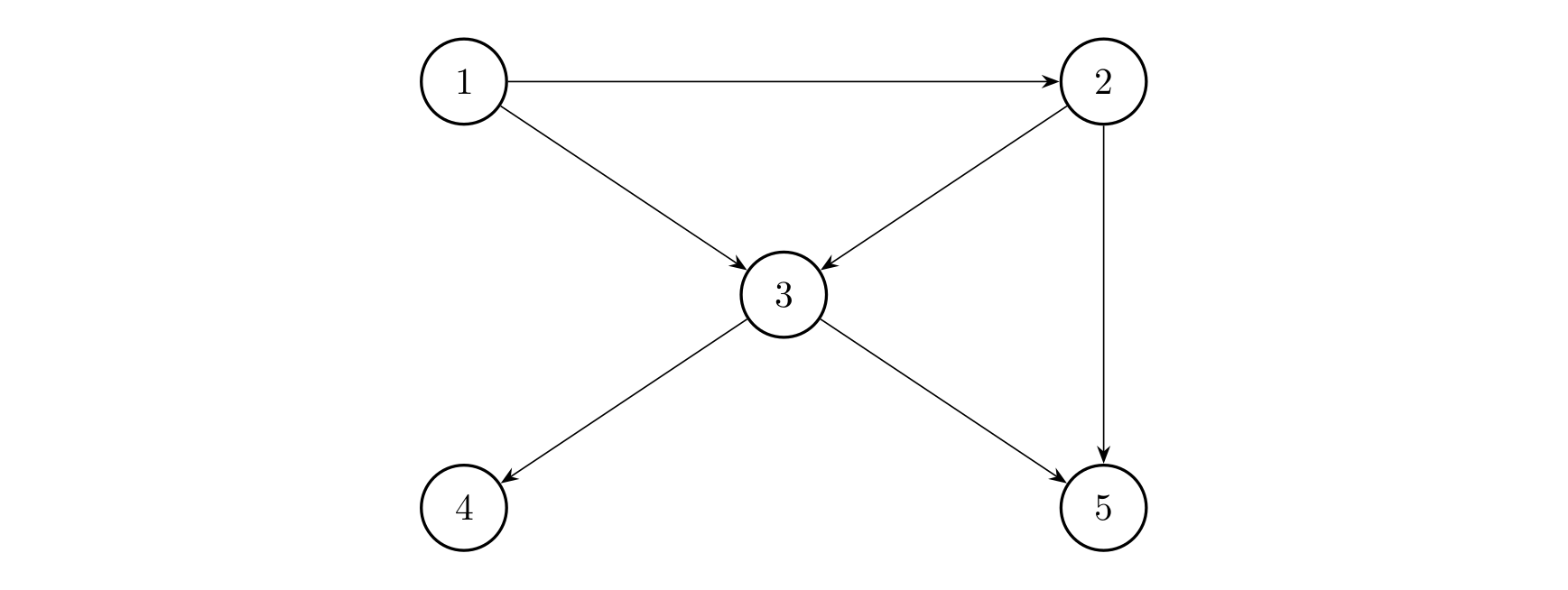
顶点 可达

顶点 可达

顶点 可达

顶点 都只能到达自身。

所以这张图的连通数为 。

给定一张图，请你求出它的连通数

对于 的数据，。

解答

思路是好想的，就是最开始的时候复杂度想错了结果复杂度是对的(っ °Д °;)っ

思路就是先缩点，然后跑拓扑排序。

我们使用 bitset 求出每一个点可以被哪些点到达。最后统计即可。时间复杂度目测 ，但是为什么能过呢？虽然 ，但是还有时间 300ms 限制就是了。

但是交上去发现跑的飞快，只有 77ms 也就是了。

P4899 [IOI2018] werewolf 狼人 Master

题目大意

在日本的茨城县内共有 个城市和 条道路。这些城市是根据人口数量的升序排列的，依次编号为 到 。每条道路连接两个不同的城市，并且可以双向通行。由这些道路，你能从任意一个城市到另外任意一个城市。

你计划了 个行程，这些行程分别编号为 至 。第 个行程是从城市 到城市 。

你是一个狼人。你有两种形态：人形和狼形。在每个行程开始的时候，你是人形。在每个行程结束的时候，你必须是狼形。在行程中，你必须要变身（从人形变成狼形）恰好一次，而且只能在某个城市内（包括可能是在 或 内）变身。

狼人的生活并不容易。当你是人形时，你必须避开人少的城市，而当你是狼形时，你必须避开人多的城市。对于每一次行程 ，都有两个阈值 和 ，用以表示哪些城市必须要避开。准确地说，当你是人形时，你必须避开城市 ；而当你是狼形时，则必须避开城市 。这就是说，在行程 中，你必须在城市 中的其中一个城市内变身。

你的任务是，对每一次行程，判定是否有可能在满足上述限制的前提下，由城市 走到城市 。你的路线可以有任意长度。

• 保证图连通，无自环、重边
• 对于每个

解答

因为题目限定了经过的点的范围，所以可以想到生成树或是重构树。而因为我们要求经过一些范围的点能够到达哪一些点，所以考虑重构树。

我们定 为 经过所有 的点能到的点的集合， 为 经过所有 的点能到的点的集合。现在我们要求的是 是否 。

那么我们建一棵重构树，树上边权为两个点的点权的最小值。然后对其建最大生成树的重构树。容易发现，点 能到达的点的集合为含有 的边权 的连通块，即一直向上跳 所能到达的最远的点使 的子树的所有点权 。此时这个点所包含的 dfn 范围就是集合 了。

点 的同理。建一棵树上边权为两个点的点权的最大值的最小生成树的重构树。然后也是跳，即得到 。

最后，你得到了两个区间。可以使用可持久化线段树求得 。